{Graduating} to The Next Level of Numbers

Infinity Is Not A Number

I recently tried to explain infinity to my children. Well, to my six year old and my four year old, since I figured it’d be a waste of my breath to explain infinity to the two year old. (Honestly, her understanding of even the first few numbers is rather suspect). For a while I thought they had it down. I’d ask what infinity was — was it a number? “No, it means there’s always more numbers!” they’d respond, as dutifully as the Von Trapp kids doing a roll call.

But it’s one thing to comprehend the “concept” of infinity: that you can always add one more to something, and a completely different thing to try and comprehend the vastness of really, really big numbers whose existence is a straightforward implication of said infinity.

When you are first learning to count, 10 is the biggest number you know of. Eventually you learn about 100, 1000, perhaps even a million. These are all numbers you can fathom counting to. But pretty quickly you encounter numbers that are impossible to count out loud. You know of their existence not by the intimate process of traversing every number before them, but by the formal process of simply adding a few more zeroes.

These are numbers that boggle the mind. Consider googolplex, or googolflex, in the parlance of my four year old. (By the way, that’s not a misspelling. The number, unlike the company, is actually spelled with the “ol” at the end). A googol is 10 raised to the power of 100 (i.e., 10¹⁰⁰) — that is, 1 followed by 100 zeroes. A googolplex is 10 raised to the power of a googol (i.e., 10^{10^100}) — that is, 1 followed by a googol zeros.

Where did the names googol and googolplex come from? According to Wiki:

In 1920, Edward Kasner’s nine-year-old nephew, Milton Sirotta, coined the term googol, which is 10¹⁰⁰, then proposed the further term googolplex to be “one, followed by writing zeros until you get tired”.

That’s a pretty brilliant definition by young Milton.

So just how big are a googol and a googolplex of something? Well, you can write down the number googol by simply filling a sheet of paper with 100 zeros. You could do it rather quickly, in fact. But what about writing down a googlplex on a sheet of paper, or perhaps a book, by listing out 1 followed by a googol zeros? Not possible. Why?

Some estimates put the total number of atoms in the universe at 10⁷⁸. Since a googol is 10¹⁰⁰ this means there aren’t even a googol atoms in the entire universe. This means that even if you were able to write each zero using a single “atom of ink” you’d be 10²² atoms short of finishing the job before you’d used up the entire universe’s supply.

This is the power of exponentiation, by the way. 10¹⁰⁰ is BIG – more than the number of atoms in the universe, in fact. But 10^{10^100} is beyond anything you can comprehend.

Numerical Relativity

We often use the time it takes to count to some number as a proxy for its size. But of course this time is relative. If you are trying to crack a physical safe, say one with 60 numbers on the dial, which requires a sequence of 3 particular numbers, you must try up to 60 x 60 x 60 = 216,000 possible combinations. Even if you could try one combination every second (which seems unrealistic), you’d have to sit at said safe for up to 60 hours to run through them all. For a would be thief, 216,000 is a lot of combinations.

On the other hand, if we replace “safe” with an “encrypted file” on a computer, you could run through 216,000 possible combinations for a password in the time it takes for me to type out the period at the end of this very sentence.

In a digital world, 216,000, or 2.16 x 10⁵ in scientific notation, is a piddly number, because computers can “count” so much faster than we can.

Because computers can count so fast modern encryption schemes must be safe even if people can try a LOT of combinations. How many? If you want to try to crack open a digital file using the latest encryption scheme you may need to try something like 10⁵⁰ combinations (which is, btw, the square root of a googol). Oh no, sorry, that was for computers running in 1991. If you are trying to crack open a digital file in 2018, you’ll need to try about 10²³⁰ combinations (which is, btw, a little more than a googol squared). ¹

It’s not just counting, though, that we use to intuit the relative size of numbers. Counting is a temporal process. We also use space to think about numbers. If you need to picture eighty thousand people, think of a packed college football stadium. If you need to picture way, way, way less than a million people, just think of the mostly empty National Mall during the last presidential inauguration.

Of course the biggest space we know of is the universe itself. We might try to imagine really large numbers by dividing the entire universe up into little regions and filling those regions with something we are trying to count.

You’d think it a fool’s errand to divide space up into a finite number of “smallest” regions. We tend to think of space as being continuous, and thus continuously divisible. But thanks to rascally old quantum mechanics physicists are able to divide space into a smallest possible unit of volume (or, at least, they assume they can). This smallest possible unit of space is called the Planck volume, and it’s unfathomably tiny. It is equal to about 4 x 10^-105 cubic meters. In case that is impossible for you to imagine, the volume of a hydrogen atom is about 1 x 10⁷³ Planck volumes, which I’ll refer to as Planck cubes as the plural of volume is just weird to read/write. According to some very rough calculations done by random folks on the internet, the visible universe has a size of 8 x 10¹⁸⁴ Planck cubes.²

Recall that a googolplex has a googol zeros. This means that if you tried to write out a googleplex by sticking a zero into every Planck cube of space in the whole of the visible universe you’d run out of room after about 200 zeroes. Meaning you’d still have a googol minus 200 zeroes remaining. But subtracting 200 from a googol is like taking away a few kids from the Duggers — you still have an absurdly large number (of kids) at the end of the day that is pretty close to the original number you started with.

The next time you look up into the nighttime sky and contemplate all that vastness remember that next to a googolplex, the seemingly infinite size of all that space is a rounding error.

To Graham’s Number, and Beyond

Scientific notation goes a long way to helping us represent large numbers like a googol and even a googolplex. But at some point further down the number line it fails to keep pace with the ever growing size of the numbers it intends to represent.

Consider, for example, Graham’s number. Graham’s number is so big that you can’t write it out using 10^x or 10^{10^x}, like you can with googol or googolplex. Recall that writing out a number as 10^x, for some arbitrary number x, is a more compact way of representing said number. 1,000,000 is 10⁶. A googol is 10¹⁰⁰ instead of 1,000,000,..88 more zeroes…000,000. And a googolplex is 10^{10^100}, instead of 1,000,000…a googol more zeroes…000,000.

But imagine you didn’t know about exponentiation, which is the technical term for raising some number (10, say) to some power (e.g., 2, 3 or 10¹⁰⁰). You’d have no way of representing a googolplex with numbers — you’d have to resort to defining it as “one, followed by writing zeros until you get tired,” which seems less than ideal for anyone older than 9.

In other words, without understanding exponentiation, you have no real way to express some really big numbers in a way that would allow you to meaningfully define and manipulate them.

So it is with Graham’s number. You need a new kind of operation (actually, a bunch of new operations) to get at Graham’s number.

What the hell am I talking about — a new kind of operation?

Consider the following operations: addition, multiplication, and exponentiation (yes, there is also subtraction, division and logarithms, but for our purposes these are just different kinds of addition, multiplication, and exponentiation).

Addition is the first kind of operation we are exposed to. We add apples or whatever.

Then we learn multiplication which is just “repeated addition”. 1+1+1+1+1 = 5 x 1 = 5.

Then we learn exponentiation which is just “repeated multiplication”. 2 x 2 x 2 x 2 = 2⁴ = 16.

Well, we can now define an operation called tetration, which is just “repeated exponentiation”.

If you see 3³, you know it means multiply 3 three’s together (repeated multiplication): 3 x 3 x 3 = 27. For tetration, the notation has the “power” on the left. ³3 means something totally different than 3³. It means, 3^(3^3). (That is, raise 3 to the third power, and raise that third power to a third power…).

Tetration allows you to write some really big numbers rather compactly. For example, remember how 3³ is just 27? Well, ³3 = …wait for it… 7,625,597,484,987. If that seems unimpressive, consider that ³9 = 9^{(9^9)} is 4.28125 × 10^369,693,099.

Sometimes tetration is called a power tower, since you get a “tower” of exponentials.

See the tower of a’s?

Please try to fathom what happens when instead of a 3, we append a 100 on the front of that bad boy: ¹⁰⁰9. Actually, don’t. I need your mind intact while we finish this out.

Good news: you learned about a new mathematical operator — tetration (aka power towers)!

Bad news: Graham’s number is so big that even those fancy new power towers won’t do the trick. If it takes exponentiation for one to write out a googolplex without using up all the atoms in the universe, it takes something much more powerful than even tetration to write out Graham’s number without using all the atoms in a googolplex universes.

Luckily, we can proceed to higher yet levels of operation. After tetration we have pentation, which is just “repeated tetration.” The next level is called hexation, which is, say it with me now, “repeated pentation.” I’m not going to explain how pentation and hexation work because we are already getting bogged down in too many new things for me to expect most readers to follow me further down. However, if you are interested in learning more about how pentation and hexation actually work, I would highly recommend this excellent (but rather lengthy) Wait But Why post, which covers basically all this big number stuff in much more gory detail. In fact, it was in that post that I first learned about Graham’s number.

For our purposes we only need to get the gist of the idea of ever increasing levels of mathematical operation. And we also need to appreciate that as we go up to higher levels of operation the numbers that get spit out of even the simplest formulas using these operators get ginormous.

To get to Graham’s number you merely need 64 new operations. Let’s pause for a moment. Until a few minutes ago you’d likely lived your entire life assuming that addition, multiplication, and exponentiation were the only mathematical operators that existed (along with their cousins subtraction, division, and logarithms). Then I introduced you to a new operation: tetration. And I showed how powerful tetration is in generating really big numbers from rather compact formulas: whereas 3³ is just 27 (using dumb old exponentiation), ³3 is 7,625,597,484,987 (using tetration).

Now I’m telling you there are many, many more mathematical operations beyond exponentiation. And we need 64 of them to represent Graham’s number.

Ok, can I at least show you what Graham’s number looks like?

Here’s a visualization of the recursive formulation of Graham’s number:

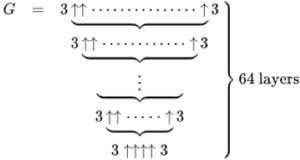
Congrats, you are staring at a well defined representation of a number that makes googolplex look as big as “three”. For each term in the above stack, a different number of arrows corresponds with a different level of mathematical operation (e.g., the four arrows at the bottom represent hexation).

Ok, now that we’ve discussed Graham’s number, I feel like I should mention that Graham’s number, in all its enormity, isn’t even the biggest number we know about. There are others, like one with the peculiar name Tree(3), which dwarfs Graham’s number, much like Graham’s number dwarfs googolplex. You need a whole new kind of mathematical operator to represent Tree(3), which I definitely won’t be discussing here (in part because I haven’t bothered to learn it myself yet).

Lucas’ Number

I recently asked my son if there was a “biggest number.” Yes, he said to my dismay. Googolflex.

Honestly, it felt like I’d completely failed him as a parent. I mean, I could sort of understand him forgetting the whole “infinity means numbers go on forever” thing, because what is “forever,” anyways, especially to a four year old? But that he’d staked his claim on googolplex — that pedestrian number that anyone with half a brain could scribble down with a mere two exponents — as the closest to infinity that we could get, that was too much for me to bear.

That’s when I told him about Graham’s number. I explained, without the whole digression on new mathematical operations, that Graham’s number was WAY WAY WAY bigger than googolplex.

And that’s when I had the brilliant idea to invent a new number for him to carry around in his little mind (and his little heart): Lucas’ Number. It’s easy to write down. It’s defined as follows:

Lucas’ number = Graham’s number + googolplex

Bigger than Graham’s number. Dwarfing googolplex. And a number he could call his very own. A number that, should he forget that infinity is not an actual number and instead default to reaching for some largest number by reflex, would at least be almost as mind boggling as infinity itself.

Footnotes:

[1] This assumes you need to run through every possible “password” needed to crack a modern encryption scheme — but in reality you can use shortcuts, so the true number of combinations you need to try will be smaller. Still, they will dwarf 216,000 by many, many, many 0’s.

[2] Keep in mind the “visible universe” is different than the “actual universe” — because there are parts of the universe that are so far away that their light can’t reach us. If you can see something in the sky though, it’s safely within the “visible universe”.