Quantum Mechanics, Explained – Part 2: To Understand Crazy, You Have to Think Like Crazy

In Part 1 of this post we learned about how crazy quantum mechanics really is. Now to understand crazy, you have to think like crazy. And that means considering possibilities that would seem completely ludicrous to anyone rational, or to anyone who had never learned about quantum mechanics.

Our task then is to consider something really, really crazy to help us make sense of quantum mechanics. What is the crazy idea we are going to be considering? That where Einstein’s theory of relativity is built on a fundamentally new conception of space and time, quantum mechanics is built on a fundamentally new conception of probability.

1. A New Kind of Probability

So you may have heard that quantum mechanics is a probabilistic theory. That is, it doesn’t tell you exactly where electrons or other quantum objects are at all times, only the probability of finding them in a given location at some future time. Of course, physics is no stranger to theories relying on probabilities. Remember the “Laws of Thermodynamics” you learned somewhere along the way? Well those are built on arguments from probability. In fact, physics majors usually learn thermodynamics as part of a broader course called “Statistical Mechanics.”

If physicists have been dealing with probabilistic theories for hundreds of years, why do people make such a big deal about quantum physics?

It’s true that quantum physics is based on probability. But unlike statistical mechanics, which is based on the same kind of probability theory you’d use to calculate the odds of a winning poker hand, quantum physics is based on a different kind of probability theory. One that cannot be reconciled with classical (e.g., Newtonian) physics.

What do I mean?

Imagine I have a pair of coins. I tell you they are magic. What’s so magic about them? If you flip each one of them separately, they behave just like regular coins. Half the time they show heads, the other half they show tails. But, if you flip them both at the same time, they always show either heads-heads or tails-tails. They never, ever, land with one coin showing heads and another coin showing tails.

These are my magic coins. They are the ones I found on Google labeled “licensed for reuse.”

Clearly, something fishy is going on with these coins. You suspect there’s some trick that, if revealed, would totally explain the “magical” results.

There is a trick, I tell you: The coins don’t obey the usual laws of probability.

Cue the skepticism.

Bear with me for a moment. Here’s how my coins “work:” one coin has a 50 percent chance of heads and a 50 percent chance of tails. The other coin has a 50 percent chance of heads and a -50 percent chance of tails.

Did you catch that? I snuck in a minus sign.

What the hell does a “negative fifty percent” chance of tails mean?

OK, I’m playing a bit fast and loose here. The laws of probability that my coins obey are slightly more complicated. In fact, each individual event (one coin landing heads or tails) gets assigned a number, which I’ll just call a “probability amplitude” because I can, and those numbers can be positive or negative.

But, if I want to get an actual probability out of my theory, I have to do something to get rid of any remaining negative numbers (i.e., take the absolute value or square some number).

Because any theory that spit out negative probabilities would be completely insane.

I’ll spare you the math and give you the gist of how my weird probability rules explain my magic coins.¹

If you want to calculate the probability of some event happening that can only happen one way, my silly new probability laws change nothing. My coins still land heads-heads or tails-tails 25 percent of the time. But if you want to calculate the probability of some event happening that can happen multiple different ways, my laws can lead to different results than the usual probability theory. Why? Because when you do a probability calculation involving different ways of some event happening those negative numbers can wreak a little havoc. I don’t know if you’ve heard, but sometimes when a positive number and an equal and opposite negative number love one another, they get close and suddenly… BAM… they cancel each other out.

If we want to calculate the odds of the event “one coin is heads and one coin is tails,” we have to consider that it can happen two ways: coin #1 is heads and coin #2 is tails OR coin #1 is tails and coin #2 is heads. And when you actually do that calculation (using the probability amplitudes I provided), the probability amplitudes from these two possibilities cancel one another out.

Again, you don’t really need to understand how the probability calculation works, only that this whole “canceling” deal cannot, will not, and never has happened in classical probability theory where all numbers involved are always positive forever and ever amen.

I know these magic coins sound absurd. Negative probabilities, or negative “probability amplitudes,” as the case may be, sound very, very contrived.

But, apparently, nature is absurd and contrived. Because the explanation I just gave for these magic coins is (at least in spirit, if not details) how quantum physics actually works.²

2. The Double Slit, Explained

This is Schrodinger’s equation:

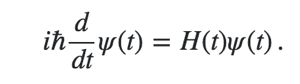
Schrodinger’s equation is the fundamental equation in quantum mechanics, the way that F=ma is the fundamental equation of classical mechanics. It’s a beautiful equation, but also a strange one. It has that “i ” — an imaginary number representing the number formerly known as

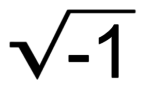
Let’s compare how one uses Schrodinger’s equation with how one uses Newton’s classical equation, F = ma. Newton’s equation is straightforward to use: you stick in some initial data about a particle and it spits out the path that the particle will trace in space and time.

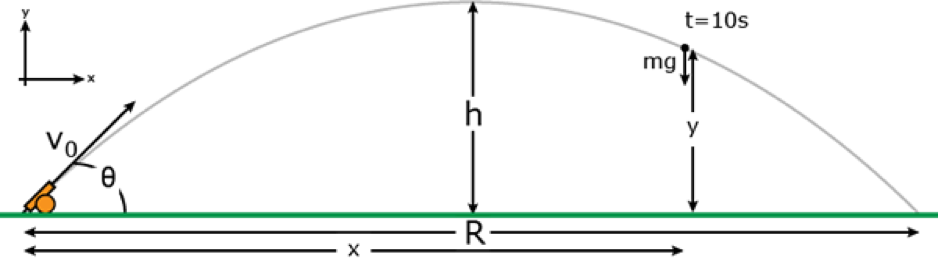
Using F= ma you can calculate the path (shown in grey) a projectile shot from this adorable little orange cannon will take, so long as you know the angle it was fired at () and it’s initial velocity (V0).

Schrodinger’s equation does no such thing. It doesn’t give you the path an electron (or other quantum particle) will take. Instead, this equation takes in inputs and spits out probability amplitudes. You know, the ones I just used to make my magic coins work. To remind you, probability amplitudes are almost the probability for an event to happen, but unlike actual probabilities they can be negative.³

Here is how quantum mechanics works. You take Schrodinger’s equation, you put in some things about the system you are interested in (the mass of the particles, etc.) and then you solve it to get a set of probability amplitudes for various intermediate outcomes. Then you combine the numbers for those intermediate outcomes as needed to get a total probability amplitude for some outcome. And then you do something to make sure that total probability amplitude is positive and, also, a real number.⁴

It’s really just a more complicated version of what you’d do to calculate the odds for (non-magic) coins to show heads or tails, or for a set of dice to show a particular sequence of numbers. Except, as we saw already, the underlying probability theory is different and so you can get bat-shit crazy results like electron’s never being in some location that, classically, they should be free to go.

Let’s return to the infamous Double Slit experiment with electrons. You can use Schrodinger’s equation to assign probability amplitudes to various “classical” paths that the electrons can take, first from the source to each slit, and then from each slit to the screen.

This is an example of various possible paths an electron could take from A to B: either going from A to slit 1 to B, or from A to slit 2 to B. In practice you would need to consider many other possible paths too.

To calculate the odds that an electron leaving point A (the electron gun) arrives at, say, point B on the screen, you do a calculation that involves combining these intermediate contributions.

It turns out that some of these paths get assigned negative probability amplitudes (because that’s how Schrodinger rolls). If you get two paths with equal and opposite values, they will cancel each other out engage in a form of numeric nihilism. The result is you will have a 0 percent probability of seeing the electron in some locations on the screen.

And this is how we get those bands where electrons never land on the screen.

Because quantum physics is based on a completely new theory of probability that allows for negative probability (amplitudes) that can sometimes cancel out positive probability (amplitudes).

3. It’s Still Weird AF

The results of the Double Slit experiment are often interpreted as demonstrating that the electron is taking all the paths to some location on the screen and we observe a sort of “net result” of all those paths. How else would the probability of seeing it at some location depend on the odds of it traveling along different paths?

From this strange interpretation, you are but a hop, skip, and a jump away from saying Schrodinger’s Cat is both dead and alive before you check on the poor thing.

Of course, “all possible paths” or “dead and alive” also ultimately fail as explanations. If the cat is both dead and alive, then we don’t have some new quantum phenomena, we just have two cats in a box, one of which happens to be dead.

Whatever the electron (or the cat) is doing, it would appear that we just don’t have a good way of understanding it, intuitively. It would seem to exist as some new logical state: not A OR B, not A AND B, but A ? B, where this new mystery logical relation has no classical counterpart.

Recall that I said quantum mechanics is much weirder than relativity. Part of that is a function of the kind of math involved. In relativity one can always make an appeal to geometry. If you ask me to explain how a four dimensional spacetime can be curved in relativity, I can appeal to your intuitive understanding of how 2D surfaces curve in our 3D space. You won’t walk away with a complete picture of relativity—for that you’d need to understand a lot of technical machinery. But you would feel as though you understood it a little better.

In quantum mechanics, we are being asked to rethink not geometry, but logic itself. We have no way of visualizing what is going on.

As Feynman said, we aren’t any closer to explaining away the mystery. But hopefully you have a new way of thinking about quantum physics that you can leverage to better understand other strange quantum phenomena.⁸ More on that in a future post.

Footnotes:

⁴  [WARNING: long footnote] I claim that you can explain the behavior of my magic coins by assuming they obey different rules of probability. How so?

With “normal” coins, each coin has a 50 percent chance of landing heads or tails and the odds for outcomes with two coins are calculated by combining the odds for each coin landing heads or tails. What if we tried, for the hell of it, to assign a “negative” probability to some outcome. Like, say one of the coins has a 50 percent chance of landing on heads and a –50 percent chance of landing on tails. For the moment we won’t worry about what that actually means. We are just doing math.

Now I tell you to calculate the odds of getting heads-heads, tails-tails and of getting one coin showing heads and one coin showing tails (doesn’t matter which one) when you flip both the coins.

We can build a little tree to figure out the odds:

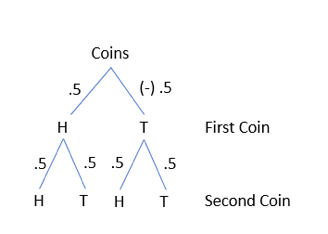
Each individual outcome is assigned a probability (0.5 means 50 percent). Note the little minus sign (-) in front of the 0.5 along the First Coin is Tails part of the tree. This will turn out to have serious consequences for what can happen with the coins.

Let’s calculate the odds of various outcomes. For heads-heads or tails-tails, there is only one way for this to happen. So calculating the odds is very straightforward.

Odds both coins are heads = 0.5 First coin is heads * 0.5 Second coin is heads = 0.25 or 25 percent.

For the tails calculation we get -0.5 *0.5 = -0.25. But because of our rule that we have to remove the minus sign to get an actual probability, the probability is still (+) 25 percent.

But, look what happens for the outcome of one showing heads and one showing tails. In this case, there are two ways to get one heads and one tails, and we have to consider both in calculating our probability. That is, we calculate numbers for both ways of getting heads and tails and then add those numbers together. I’ve highlighted the two relevant “branches” of the tree here.

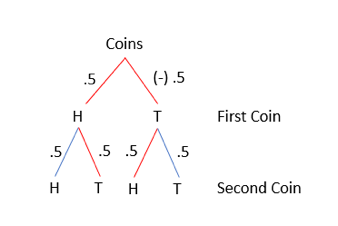
Odds of path on the left =  0.5 (First coin is Heads) * 0.5 (Second Coin is Tails) = 0.25

Odds of path on the right = -0.5 (First coin is Tails) * 0.5 (Second Coin is Heads) = -0.25

If we add these two different ways of getting one heads and one tails together we get:

Odds of one coin being Heads and the other coin being Tails = 0.25 + -0.25 = 0

ZERO. ZIPPY. ZILCH.

There is no possibility of seeing a heads-tails combination on these magic coins. Because negative probability amplitudes and math.

Footnotes

1 To be clear, these coins are not a real quantum thing. Not only would coins be too large to behave like quantum objects, I’m pretty sure you could find some inconsistencies in the way I’ve defined things here. It’s ok, because it’s only meant as a tool to see how negative numbers can be problematic if you let them loose in probability theory.

2 In my magic coin example I only used positive and negative real numbers. But in quantum mechanics the probability amplitudes can be complex numbers. That is, numbers that include that funny little i that we saw in Schrodinger’s equation.

³ You definitely do not want imaginary probabilities. That seems like the sort of thing that could cause a hole in spacetime to open up and suck us all in.

⁴ I should note for the record that this way of thinking about quantum mechanics isn’t something I dreamed up. It’s a (slightly dumbed down) version of a viewpoint put forward by some the preeminent physicists who study the foundations of physics. In particular, I learned the ideas here from the highly entertaining quantum information theorist Scott Aaronson. If you want an even nerdier version of the arguments I presented above, in comic form, click here.