
Prompt Images
By now, surely you’re recovering from your sugarshock candy coma, after indulging in one of this country’s most sacred yearly rituals. A day in which young children and grown adults alike engage in a bit of cosplay and consume a cacophonous mixture of confectionaries—chasing pre-portioned bites of Snickers with handfuls of Runts.
Personally, I’m a bit split on Halloween—I’m not a fan of spooky couture, but I’m also in no position to turn down the chance to stock up on several full pound bags of M&M’S without the shame that would usually attend such behavior. Truth be told, my favorite “candy” holiday isn’t even Halloween; it’s Easter, on account of that being the one time of year when Reese’s finally sells the perfect ratio of peanut butter to hard candy shell in its Reese’s Pieces Eggs.
Still, the occasion of Halloween does provide me with a good excuse to bring attention to a particular monster that has mostly gone unnoticed over the last few decades outside of a very niche audience. The reader should be warned, however, that this monster is unlike anything he or she is likely to have encountered. You’ll need no pitchforks or silver bullets or wooden stakes—only curiosity and a bit of patience to help me track it down.
And lest anyone accuse me of a kind of literary bait and switch, I’ll just come right out and say it. The monster we seek is mathematical in nature. But as far as I’m concerned, it’s still as fantastical as anything from the pages of Stoker or Shelley.
I. Fascination with The Monster
In the 1970s, two mathematicians named Robert Griess and Bernd Fischer made independent discoveries—or rather, predictions—of a truly bizarre mathematical object. Both men predicted that this object should exist, though it wasn’t seen until 1982, when Griess finally figured out a way to write it down.
If it seems odd that mathematicians could predict the existence of some mathematical object, some equation or geometric shape or sequence of numbers, without already having this object in hand, it is only because you have yet to comprehend the strangeness of this object for yourself.
In an early paper, Fischer referred to this object as the Friendly-Giant, but the name didn’t stick. It eventually became known as The Monster. Cue creepy music and an ominous thunderclap.
One of The Monster’s more illustrious admirers has been the mathematician John Conway of Princeton University. Conway is approaching 80, with a full head of middle-parted brown hair, which he often pairs with a wiry grey beard.
His hairstyle is a little reminiscent of The Wolverine, no? (credit PRINCETON UNIVERSITY, OFFICE OF COMMUNICATIONS/DENISE APPLEWHITE)
Conway’s mathematical interests, like his coiffure, may be best characterized as eclectic. In addition to contributions in technical research areas like combinatorics, group theory, and topology, he’s also done work that has more of a populist appeal. He is most famous for creating “The Game of Life,” a two-dimensional simulacrum of the world in which a pattern of black dots migrates across a grid according to some simple logical rules. Watching the pattern of dots evolve—as individual dots undergo processes of “birth” and “death”—one eventually observes fascinating creatures that appear to be moving through their world with a sense of purpose, a sense of life.
Conway became interested in The Monster in the late 1970s, before it had been observed in the wild. In the mid-80s, he published several important papers that helped elucidate the original work done by Griess and Fischer. Those particular elucidations aside, Conway is still perplexed even 30 years later.
“The one thing I’d like to know before I die,” he told an interviewer in 2009, “is why The Monster group exists.”
It would surprise no one to hear a biologist express bafflement about some newly discovered species. Why should this creature have four toes and not five? Why an eye where its ear should be? There are an uncountable number of evolutionary contingencies to consider. Bafflement is a perfectly reasonable mental state for a biologist.
But mathematics is supposed to be different. There are no contingencies in math. No what ifs. Only if, thens.
In such a rigidly predetermined system where one starts with axioms and follows reason wherever she may lead, how can there be any room for surprise?
II. A Brief Mathematical Interlude
Formally, The Monster is what mathematicians refer to as a “group.” In order to get some traction in understanding The Monster, then, we must first understanding a few basic things about groups.
The first inklings of the modern concept of a group are found in the work of Evariste Galois, a Frenchman who, within his brief 20 years of life, managed to get himself arrested for seditious speech against a king, partake (and die) in a duel, and build the foundations of one of the most important actors in modern mathematics—the group. Almost 200 years after Galois, group theory is a staple in the diet of any budding mathematician.
So what is a group?
In essence, a group is a set of mathematical objects along with an operation that can be performed on the mathematical objects, such that performing the operation on any two objects results in another object that is also in the set. Before we get lost in conceptual mumbo jumbo, let’s break it down.
Consider the set of several integers: {1,2,3} and the “operation” of addition. Does this set together with this operation form a group? No. Why? Because if I add any two elements in this set, the result must also be in the set? And since 2+3 = 5 (which is not in the original set), this is NOT a group.
On the other hand, consider the set {-1,0,1} and the operation of addition. This is, in fact, a group because adding any two numbers in this set results in a number that is also in the set (-1 +1 = 0, 0+1 = 1, -1 + 0 = -1). (There are actually additional properties a group must have that we won’t get into—these also happen to be satisfied by this example).
Now consider a group motivated by geometry, specifically, the geometry of a square:

We can ask, what are the things we can do to this square that leave it looking the same, in a geometric sense? Well, we can rotate it by 90 degrees, or by 180 degrees, or by 270 degrees. We can also rotate it by 0 or 360 degrees (which amount to the same thing). All these leave the square unchanged in terms of its location and orientation on the page. Mathematicians say these actions are symmetries of the square.
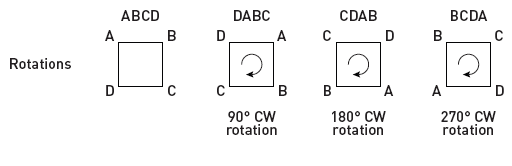
What does this have to do with groups? Well, let G be the set of “rotations” of the square that leave it’s position and orientation preserved. G = {R90, R180, R270, R360}. We then define a “group operation,” denoted with an asterisk (*), as doing two rotations back-to-back. So, for example, R90 * R180 = R270.
That is, performing a rotation of 90 degrees followed immediately by a rotation of 180 degrees results in the equivalent of rotating the rectangle by 270 degrees all at once. This is a group, because any “combination” of rotations results in another rotation that is already in the set.
If you are currently wondering what “a rotation by 90 degrees” is—well, you are now in a position to see how abstract the concept of a group can get.
R90 isn’t a number or a shape. It actually represents “the process of rotating a square by 90 degrees.” This is the whole point of group theory: to cast the widest net possible. Let everything that can be a group, be a group. If you want to make a group out of: {a dolphin, a chair, Anthony Hopkins, and a potato}, so long as you are able to define some meaningful abstract “operation” on the objects in this set (though don’t ask me what that might possibly be in this case), and so long as this absurd construction obeys the other rules that groups need to obey—have at it.
It’s your Galois-given freedom.
Now the example above of the rotations of a square shows the connection between “symmetries” of geometric objects and some groups. Similar groups describe the “symmetries” of other objects like triangles, pentagons, cubes, dodecahedrons, etc., though this is a bit misleading since there are more complicated kinds of geometric symmetries that go beyond rotations of simple polygons.
Moreover, it should be clear by now that a group is its own thing, defined by its own rules. And we can talk about groups independently of any incidentally-related geometric objects. (e.g., there need not be a geometric shape corresponding to the group of {a dolphin, a chair, Anthony Hopkins, and a potato}).
If all this seems a bit like abstraction for its own sake, well it is, mostly. But, group theory also has practical applications in many realms outside of pure mathematics. In chemistry, groups help explain how electrons are distributed in the atom. In physics, groups help us understand how quarks are distributed in the nucleus. Group theory can also be used to solve a Rubix cube.
Not that any self-respecting pure mathematician worries much about “practical applications.”
III. Organizing Groups
Ever since the time of Galois, mathematicians have studied various examples of groups and tried to classify them. Why enumerate and classify groups? Because humans as a species have a tendency towards taxonomy.
We organize things. It’s what we do.
Because groups are so abstract, because they only need to follow some very basic rules, there are a lot of groups. In fact, for every number N there is at least one well defined group of size N. For example, if N=4, we already saw that there is a group of size 4 that describes the rotations of the square that preserve its symmetries.
As a simple model for mathematical taxonomy, think about the integers. There are an infinite number of integers. For every N, it goes without saying, there is an integer N. And yet you can classify integers in a meaningful way that goes beyond just listing them all (which would take you forever, because, again, there’s an infinite number of them).
One classification scheme involves dividing integers into primes and composite numbers.
A prime number is a number with no integer divisors (i.e., can’t be evenly divided by) besides 1 and itself. A composite number is a number with an integer divisor besides just 1 and itself (or, put another way, a composite number is a number that is not a prime). And all composite numbers, it can be shown, can be written as a product of only prime divisors.
With this classification system in hand, mathematicians have spent the last two millennia proving theorems about primes and composites and in the process building a field of mathematics called Number Theory that tells us all sorts of “interesting” things about numbers.
It shouldn’t be surprising then that in the 1970s, some mathematicians decided that the field of Group Theory should attempt to completely classify all groups of a particular kind—so-called “finite simple groups.” These finite simple groups may be thought of as the building blocks from which all other finite groups (a finite group is just a group with a finite size) can be made. Again, similar to how prime numbers are the “building blocks” of all the integers – since any number can be decomposed into a product of primes.
As part of this program dozens of mathematicians worked furiously over the next few decades to identify all the “kinds” of finite simple groups that could exist.
The work, when combined with earlier results in the field, culminated in a “proof” running to just under 1,300 pages, demonstrating that every possible kind of finite simple group had been identified. One researcher went so far as to organize these groups into a chart reminiscent of the the periodic table of elements:
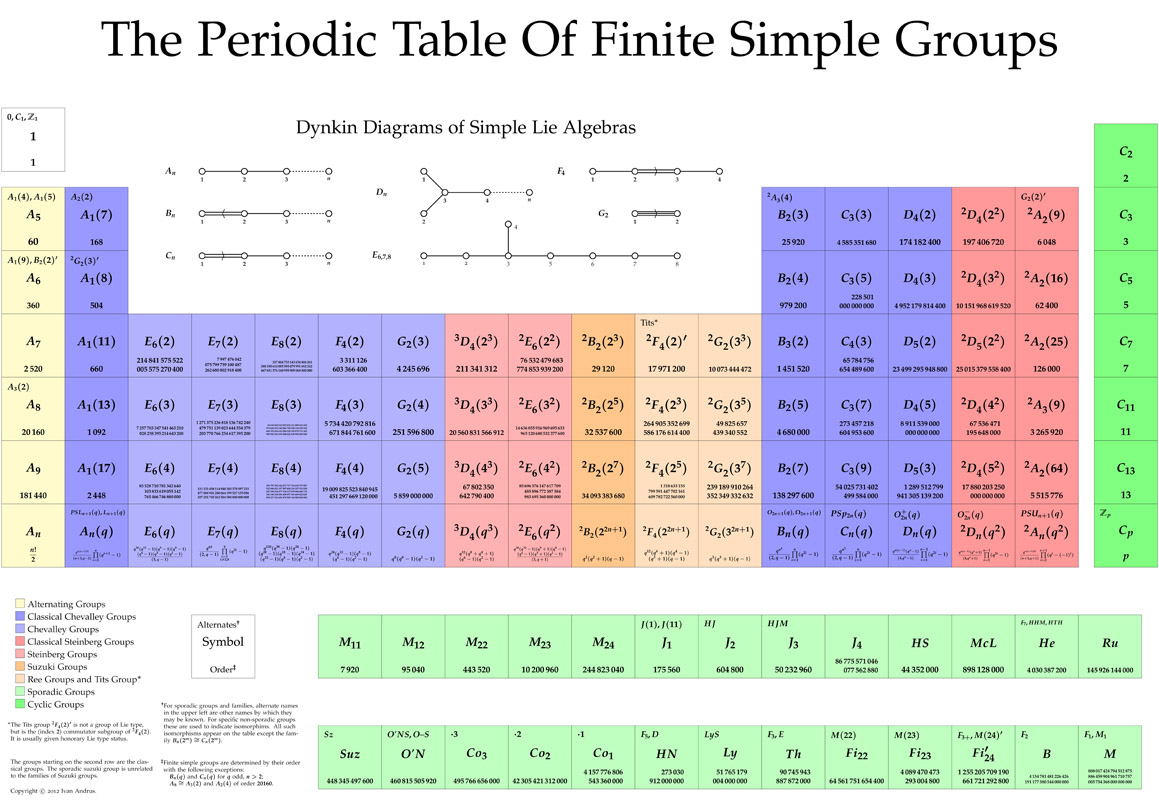
(credit: here)
To be clear, the mathematicians who worked on this project didn’t actually enumerate every possible finite simple group. Because you can always build groups out of larger and larger numbers of elements, there’s no end. (This is similar to how mathematicians in Number Theory study the properties of prime numbers, but can never succeed in listing all of them.) But, you can still show (and even prove) that no matter how large your group gets, it will fit into one of these already identified classifications.
In the final taxonomy, the researchers came up with a list that included common group structures and a set of completely unique groups that didn’t fit into any pattern. These common group structures can be thought of as groups that can be defined by simple rules, similarly to how we can define the class of primes as “numbers that are only divisible by 1 and themselves”.
The unique groups that didn’t fit into any of the common patterns were called “sporadic groups,” —scattered, isolated. We might also call them “funky” groups, because it better brings to mind their idiosyncratic nature. In a sense, they defy any kind of straightforward classification.
There are 26 funky groups, in all. Why 26 special groups that don’t match the common group patterns? No one knows.
But what’s stranger than these 26 uninvited guests into a classification system that otherwise works beautifully for groups of any size, is the nature of one of those guests in particular. Of the groups that “don’t belong”, this particular group really, really doesn’t belong. It’s in a league of its own.
Any guesses which group that is?
IV. Meet The Monster
So what exactly is The Monster group?
Well, we might think of it as a group of “rotations” of some geometric object, in the same way that the group {R90, R180, R270, R360} is a group of rotations of the square. (The analogy isn’t perfect — the elements of The Monster aren’t strictly speaking “rotations” — but it’s close enough for our purposes.)
However, our geometric intuition will be of no use here, as the object that plays the role of the “square” to The Monster group lives in a space of 196,883 dimensions.
If 196,883 dimensions seems surprisingly large, you may want to sit down for this next part.
Recall that the “size” of The Monster (as with any group) is the number of elements it has: {R1,R2,R3,R4,..etc.}. For The Monster each element (R1, R2, etc.) represents a unique “rotation” of some absurd 196,883-dimensional object that preserves that object’s symmetries. [1]
So how many elements does The Monster have? Well, whereas the “group of rotations of a square” has 4 elements, the “group of rotations of the above referenced 196,883-dimensional geometric object” has, itself,
808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000
elements (i.e., The Monster consists of the above number of different unique rotations).
First, this is an unfathomable number. It is, apparently, roughly the number of atoms that make up Jupiter. But just saying that doesn’t do the number justice.
Some astronomers estimate the number of stars in the entire universe at 1,000,000,000,000,000,000,000,000 – which is still 800,000,000,000,000,000,000,000,000,000 times smaller than the number of elements in The Monster.
The next largest sporadic/funky group, the so-called Baby Monster Group, is also quite large, with 4,154,781,481,226,426,191,177,580,544,000,000 elements. But The Monster group isn’t just double, or triple, or even 100 times its size. It is 1 with 20 zeros times larger! [2]
But even putting aside the sheer size of this thing, why this particular number? Remember, there are groups that are larger than The Monster, but they follow some common pattern. They aren’t funky. They are in some sense, ‘simple’ – in many cases just bigger versions of some earlier group.
What the hell is so special about the number 808017424794512875886459904961710757005754368000000000 ?
V. Surprising a Genius
To understand how The Monster has surprised a genius like John Conway, we might consider an analogous situation in a more “tangible” field, like entomology (the study of bugs). Imagine you are a biologist who studies a particular family of bugs, and you’ve spent your whole life trying to classify all the various kinds of bugs in this family. It turns out that bugs in this family have different numbers of legs. Many species have six legs, some species have ten, still others have twenty. Over your whole career you develop this wonderful taxonomy that is primarily based on the number of legs and you have, to this point, observed bugs in the family with as many as 100 legs! Then one day you are out in the field collecting specimens and you discover a bug that belongs to the family you study, but instead of having 6, 10 or even 100 legs, it has 4,576,578 legs. An unfathomable number, legwise. And you have no idea why it has so many.
Crazier still is that over the next three decades of your career you have yet to find another bug in that family with any number of legs between 100 and 4,576,578, or any bug with more than 4,576,578 legs. Your classification system works nice and neatly, following a sort of taxonomic logic, until you get to bugs with 100 legs and suddenly the number of legs jumps by 4,576,478 without any obvious reason whatsoever.
It wouldn’t be surprising then, if towards the end of your life you felt the most important question in your entire career was this: why does the “monster” bug exist?
If you take nothing else away from this piece, if you are still horribly confused by what exactly The Monster is, as am I, I hope that you can at least begin to understand why John Conway is so confounded by the existence of The Monster.
The Monster defies the “simple” taxonomic system that was intended to “explain” groups. It doesn’t just defy it though, it makes an absolute mockery of it. It is a bug with 4,576,478 legs in a world where every other creature has no more than 100.
VI. Why or Why Not?
To be sure, not everyone feels that the presence of The Monster is some grand mystery that requires explanation. The mathematical historian E.T. Bell was especially contemptuous of those who spent their days finding and classifying finite groups. Thirty years before The Monster was discovered, Bell wrote—in arguably one of the greatest burns in mathematical erudition:
[I]t was possible for industrious laborers little advanced beyond mathematical illiteracy to obtain almost any finite number of permutation groups by obstinate grubbing, and to find by the same dull means all the finite abstract groups in certain narrow categories which they themselves had defined, apparently with the express purpose of dignifying their calculations with an air of pseudo generality.
Bell died in 1960, but one wonders what he would have thought of John Conway with his obsession over finite groups and mathematical games.
Beyond Bell’s specific grievances with those who advance their mathematical careers by “obstinate grubbing,” others find the classification of finite groups a worthy endeavor, and yet are critical of any attempts to search for some cosmic significance in the particular size of The Monster, or in other special numbers that arise throughout mathematics or the sciences.
I’m sympathetic to the concern that if you’re not careful, questions like this can lead down the path towards numerology. But that some feature of reality may have no deeper explanation need not preclude us for searching for one.
Some people spend their professional careers time wondering how we came to exist, how this particular configuration of 1082 physical atoms came together just so, and we call them philosophers. Others spend their careers wondering how The Monster came to exist, how this particular configuration of 1053 mathematical elements came together just so, and we call them mathematicians.
But are the philosopher and the mathematician really engaged in such different enterprises? Don’t these questions share a sort of structural similarity? Some enormous group of things (atoms/abstract elements) obeying some simple rules (physics/group axioms) so as to produce a thing (our universe/The Monster) so complex that we can’t help but feel a sense of surprise, awe, and at times, even a little terror?
Footnotes:
[1] Please recall that groups are their own mathematical things, and their relation to particular geometric objects is in some ways incidental. That a particular group with 4 elements happens to “behave like” the rotations of the square that preserve its symmetry is in some sense a convenient way to think about the group with 4 elements, NOT as a way of defining the “reason” that the group with 4 elements exists. Likewise, don’t be tempted to find the “reason” that The Monster exists in said 196,883-dimensional object. It’s just a (every-so-slightly) less abstract way to think about The Monster group. And therefore, don’t expect me to try and explain what said geometric object is or what it “looks” like. You ought to know better by now.
[2] Ok, one question you might be asking right now is how mathematicians ever found a group this big – since it’s unreasonable to suspect they ever wrote down the whole thing and checked that all of its 1053 elements obey the rules of a group. Did find a way to plot it on their TI-85 calculators? No, though they may have used computers to assist them with their calculations. The short answer is, they leveraged the power of math to prove The Monster existed and to grasp many of its features without ever having to write down the whole thing. It’s not so different from how mathematicians can prove that there are an infinite number of prime numbers even though it’s impossible to write all the integers down.



