How to Think About Infinity Without Going {Completely Mad}

A Conversation About Infinity

A conversation I have from time to time with my 6 year-old son:

“Hey buddy, is infinity a number?”

“No!”

“What is it?”

“It means the numbers keep going forever!”

“Yes!”

Consider, as an example, the (positive) integers: 1,2,3…and so on. We are told that numbers are infinite. But how do we know they go on forever? How do we know there isn’t some number where the whole thing just stops?

We know that the integers go on forever because we’ve defined them to go on forever. The integers are merely the result of a simple rule: Start with 1, and keep adding 1: 1, 1+1, 1+1+1…

No matter how large a number you come up with you can, according to this rule, always add 1 more to make a bigger number. Talking about a largest integer is no less absurd than talking about a smallest Keanu in this strangely soothing GIF:

A world of infinite Keanus seems like a pretty good world.

Infinities Within Infinities

Okay, now let’s consider the set of only the positive even integers: (2,4,6,…)

This set is, like the integers, infinite. This set also happens to be contained within the set of all positive integers. In fact you can create this set by removing all the positive odd integers from the set of all positive integers:

(2,4,6…) = (1,2,3…) – (1,3,5…)

This is where our intuitive notions of infinity start to get slippery. How, for example, can you remove an infinite number of elements from an infinite set and get another infinite set? And can we say these two infinite sets are the “same size” when one of them would appear to have twice as many numbers as the other?

In the late 19th century, the mathematician Georg Cantor had a series of revelations about infinity that changed our understanding of it forever. One of Cantor’s brilliant ideas was that even though you can’t count the elements in an infinite set (like the set of integers), you can compare the relative sizes of two different infinite sets.

How can we compare the sizes of infinite sets?

Consider our above example, the set of all positive integers and the set of all positive even integers. If you label each element in a set as S1, S2, S3, etc. we see a clear “pattern” between the elements in the two sets.

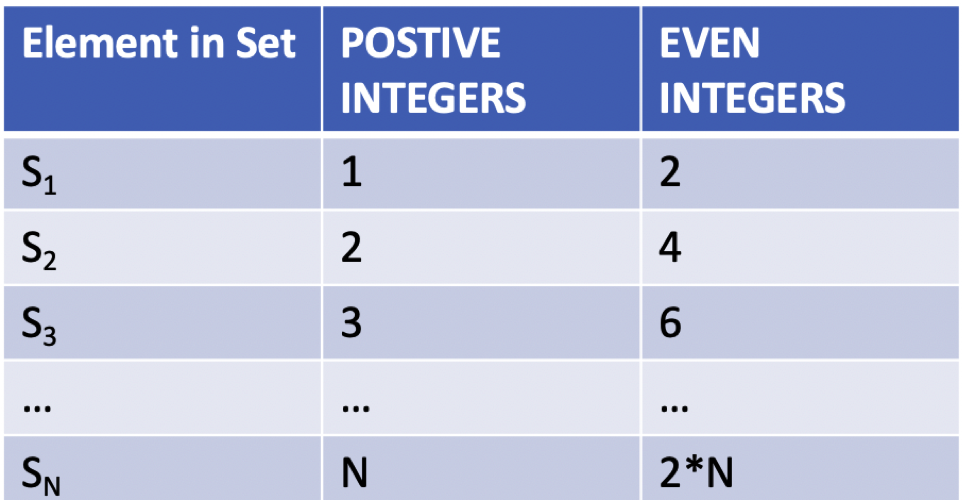
Namely, the S_Nth term in the set of all positive integers is just N, and the S_Nth term in the set of all even integers is equal to the S_Nth integer multiplied by 2.

That we have such a relation (an equation, really) means there’s a unique pairing of elements from each set. The following illustrates how the first three elements of these two sets are “paired” off:

If these were the only elements in these two sets, we could obviously say they have the same size (namely, 3). But Cantor realized that we could extend this idea to infinite sets as well. We may not be able to write down all the pairs, but we know in this case that no matter which positive integer we pick, there’s a unique positive even integer to pair it with (and vice versa).

So if all of the elements of two infinite sets can all be paired off, might it be reasonable to consider the two sets as having the same size?

Cantor believed so. And so he defined the size of any infinite set whose elements can be paired off with the positive integers in this manner to be countably infinite.

Now if all infinite sets could be paired off with the integers—that is, if all infinite sets were countable—there wouldn’t be much more to say here. But Cantor suspected that there might be other kinds of infinities.

That is, sets that are infinite, but not countably infinite.

Cantor eventually proved that there are some infinite sets whose elements cannot be paired off with the integers in the way described above. At first this may seem counterintuitive. The integers are infinite, so it would seem there is enough of them to pair off with the elements from any other infinite set. Alas, this is incorrect. Infinities apparently come in different sizes.

Cantor’s Very Clever Proof

Cantor’s proof is really clever. Like, “belongs on the list of all time best mathematical proofs” clever. And unlike proofs of many other infamous results in mathematics, you don’t need a Ph.D. to understand the gist of it.

The set we want to consider for this version of the proof is the real numbers.

The real numbers include literally any number you could think to write down, such as 10.05 or 1.0192374581245072385 or 9900.333333333333333 (with the 3s repeated forever). In other words, real numbers are not whole integers; they include the fractions and decimals between, as well.

The real numbers include the integers as a subset, just as the integers include the even numbers as a subset. But whereas we showed above that the set of even numbers and the integers are actually “the same size,” Cantor suspected that the real numbers were actually bigger than the integers. In fact, he didn’t just suspect it, he devised a way to prove it.

Recall that the integers are the prototype of a countable infinity. To say the real numbers are bigger than the integers is to imply that real numbers are not countable.

The proof can be made simpler if we focus only on the real numbers in the interval between 0 and 1. Even in this seemingly small gap between the first two integers, it turns out that there is an unfathomable amount of real numbers.

Proceeding as Cantor once had, we want to prove the following assertion:

The real numbers in the interval 0 to 1 are not countably infinite.

To prove this statement we will use a type of proof known as proof by contradiction.

In this type of proof, we assume that our original assertion is false, then demonstrate some absurd/impossible conclusion (the contradiction). This, in turn means our original assertion must in fact be true. (If this explanation is confusing, no worries, it takes time to get used to this style of proving theorems. Hopefully it will become a little more clear as we go through the proof.)

Our proof starts by assuming that the assertion above (that the reals are not countably infinite) is false. If our assertion is false, then it means the real numbers are countably infinite.

Okay, so we are starting with the statement, which we use as a starting assumption, that the real numbers are countably infinite. Again, this is the opposite of what we are actually trying to prove, but that’s the nature of proof by contradiction.

Now, if the reals are countably infinite, then there is some way to define a pairing between each integer and each real number. We might imagine this pairing as a (hypothetical) table that lists all the integers in one column and all the real numbers in an adjacent column. Each row represents one of our pairings. Part of the table might look like this:

It’s really important to realize that our table is assumed to include every single real number in the interval between 0 and 1. No reals left behind.

Okay, having constructed such a pairing in our minds, we can turn to Cantor’s clever trick for arriving at a contradiction.

Cantor’s idea is to construct a real number between 0 and 1 according to the following rules:

1. Take the first digit of the first real number in the above table and add 1 to it.
2. Take the second digit of the second real number in the above table and add 1 to it.
3. Take the third digit of the third real number in the above table and add 1 to it.
4. Take the Nth digit of the Nth real number in the above table and add 1 to it.

And so on…

In terms of our table, we are selecting the digits highlighted in yellow below, and then adding 1 to each.

For this example, the highlighted digits are 2, 0, 3, 2, 5, etc.

We are supposed to add 1 to each of these, giving the digits 3, 1, 4, 3, 6, and so on.

Now Cantor says to string all of these digits into a single number and append a “0” to the front (to make it a number between 0 and 1). Note: This number will be infinite, because we are selecting one digit from each of the rows in our infinitely long table.

So following Cantor’s prescription we create a new number, which we will call X, that starts with “0” and includes the string of digits starting with 31436. This means X = 0.31436… Clearly a real number lying in the interval between 0 and 1.

What’s the point of doing this?

Well, X turns out to have a very special property: It doesn’t already exist in the original table.

This is critical because we assumed (due to the countable nature of the reals) that the table included all the real numbers from the get-go. Whoops.

But wait, the table is infinite. How do we know X doesn’t exist in the table?

We know because of how we went about constructing X. Note that the first digit of X differs from the first digit of the first real number in our table, so X is not the first real number. The second digit of X differs from the second digit of the second real number in our table, so X is not the second real number.  The Nth digit of X differs from the Nth digit of the Nth real number in our table, so X is not the Nth real number. And so on, to infinity. In this way, X differs in at least one digit from ALL the (infinite) numbers in the original list. If it’s different from every number in the table, then its not included in the table (duh).

The reason this is so brilliant is that it doesn’t matter what specific pairing of integers and real numbers you use. This recipe will always allow you to construct a new number that is not already represented in table.

Clever, right?

To summarize, we started our proof by assuming we could pair off each of the real numbers with one of the integers. And then we “found” a real number, X, that was not paired off with any integer.

This means we found a contradiction.

And, accordingly, our assumption that the real numbers are countably infinite must be false.

But if the real numbers aren’t countably infinite, what the hell kind of infinite are they? Mathematicians refer to this as an uncountable infinity.

Regardless of what we call these infinities, the bigger takeaway is this: there is more than one kind of infinity.

Cantor’s Legacy

Cantor’s peers received his new ideas about infinity less than favorably. The eminent mathematician Leopold Kronecker, who had been one of Cantor’s teachers, called Cantor a “corrupter of youth.” The giant of 20th century philosophy, Ludwig Wittgenstein, referred to Cantor’s work on sets and infinities as “utter nonsense.”

Towards the end of his life, Cantor suffered from severe depression and was occasionally institutionalized. There’s a sort of mathematical folklore that Cantor was driven to madness after spending so much time contemplating the nature of infinity. More likely, he was bi-polar. And the stress of being constantly ridiculed by his contemporaries led to significant anguish, as it likely would have had he been working in any other field.

Cantor’s work on sets and infinity is now seen as foundational to many areas of mathematics. His critics—it turns out—were the ones spouting “utter nonsense.” But there’s another critique of Cantor’s work with which we must contend. This is the idea that Cantor, in trying to distill infinity to its most basic essence, trivialized it. That he took a concept that has, over millennia, invoked both wonder and existential dread, and reduced it to a table of numbers.

But I don’t think that is Cantor’s legacy. He didn’t so much explain away the paradoxical nature of infinity, as locate its source: in the heart of the numbers with which we are already intimately familiar. For Cantor, the integers are not just one example of infinity. They are the prototype for the simplest kind of infinity. The standard by which all other infinities must be judged.

Another Conversation About Infinity

I’ve told my son about these different kinds of infinity. Occasionally I’ll ask him to explain them to me, or to some unsuspecting guests.

“Countable infinity means you have some things and you start counting them 1, 2, 3… Uncountable infinity means you start counting 1, 2, and then you realize oops, I missed one, so you have to start again—1, 2, 3, but oops, you missed another one and you have to start again.”

As he speaks he waves his hands in a frantic manner, making chopping motions between the first and second things.

It’s hard to know if he really understands the distinction between countable and uncountable infinities, or if it’s even possible for anyone to really understand the distinction between countable and uncountable infinities with only words. In this way, he’s no different from the mathematicians before Cantor who had some basic understanding of infinity, but who lacked the analytic tools necessary to make anything other than vague pronouncements about it.

For me, whether my 6 year-old understands the precise difference between countable and uncountable infinities is not really the point. It’s that he has any interest in infinity at all. That this same boy who is primarily obsessed with turtles and Pokémon—and is generally less “math curious” than his older sister—also lights up when he talks about unfathomably large numbers and the subversive idea that there might be no end to the numbers at all.