Guns + Galois = The REAL Good Will Hunting

I. A Troubled Genius

Ever since Einstein, scientists have been a part of our celebrity culture. Neil deGrasse Tyson has over six million followers on Twitter. Sheldon Cooper, a fictional theoretical physicist on CBS’ Big Bang Theory, is a household name.

Mathematicians, however, have never had as much cache. Part of the problem seems to be that no one really knows what mathematicians do, so why bother learning any of their names? In contrast, physics, as esoteric as it can be at times, ultimately touches on tangible things we can (try) to grasp: space and time; matter and antimatter (just kidding, don’t try touching the latter—it will annihilate you).

And we, sort of, understand what these physicists do. Those of us who took at least an introductory physics course in high school have seen some basic physics equations. We get that practicing physicists work with much more complicated equations, but the endgame is still the same: solve some equations so you can understand how some ball/car/rocket/planet moves. Or whatever the hell is going on here:

 

But mathematicians? No one understands what they do. Many of us took an algebra class in high school, maybe even a calculus class in college. But it isn’t clear to us what someone who “does math” for a living would even be doing. Solving algebra equations with like 50 x’s in them? Crafting the world’s most intricate word problems?

In Good Will Hunting we watched Matt Damon’s character, the math prodigy Will Hunting, do some kind of tinker toy inspired math problem.

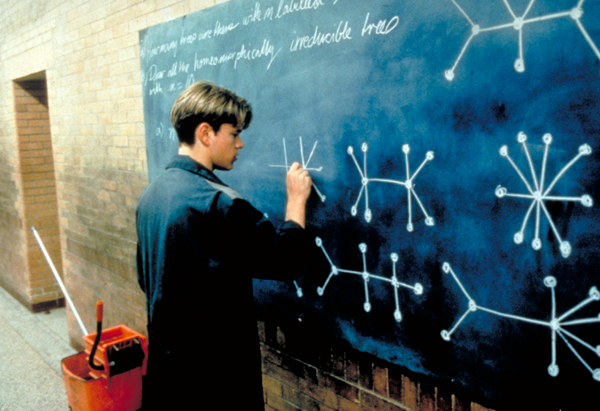
We didn’t understand what Will was doing, but we watched him do it anyways. We tolerated his eccentric behavior because we found his backstory gripping: a kid with a tragic childhood and a penchant for getting into trouble, who just happened to be a genius among geniuses.

To have any hope of understanding what mathematicians do, we require an interesting enough mathematician. Someone like Will Hunting, only real. Because seriously, no one buys that a mathematician could have arms like this.

Enter Evariste Galois (pronounced “gal-wa”), who might actually be the closest thing that history has ever had to Will Hunting. Like Will, Galois was both brilliant and deeply troubled. By the age of 20, Galois had done enough profound work in mathematics to be considered one of the all-time greats in that field. For comparison, by the time Einstein was 20, he’d done exactly bupkis. Though, in Einstein’s defense, he was only a year away from publishing his seminal: Conclusions Drawn from the Phenomena of Capillarity, his “how water moves through straws” paper. No, I kid, that paper was completely unremarkable—it would take him five more years to publish anything seminal, at the ripe old age of 26.

But Galois was more than just a genius. He was also a firebrand prone to getting arrested. Sound familiar?

And then there was that duel. But we are getting ahead of ourselves.

II. On Being French

I’ve pretty much lived my entire life without having any real knowledge of the French Revolution and its aftermath, despite my sneaking suspicion that it played a pretty big part in how the Western World has evolved since that time.

On the other hand, Evariste Galois had no choice in the matter. He was, as his name belies, very much French. He was born in 1811 and came of age in a France that was only a couple decades removed from the storming of the Bastille in 1789, which kickstarted the French Revolution. That revolution begat the following succession of power that could rival any period in the history of Westeros.

I want to be clear here—those orange dots don’t just denote changes in ruler, like your run-of-the-mill Louis XII handing the crown over to Louis XIII or whatever. No, each of those dots represents a change in the system of governance! So within a hundred years or so, France went from Monarchy (Bourbons) to Representative-ish (the National Assembly) to straight up Empire (Napoleon), then back to Monarchy (Bourbon Restoration) then to a Monarchy-Lite (Louis-Philippe), then doubled back on Empire (totally different Napoleon) and finally to a revised version of a National Assembly.

By comparison, here is a timeline of the U.S. transitions between different governing systems during that same period.

 

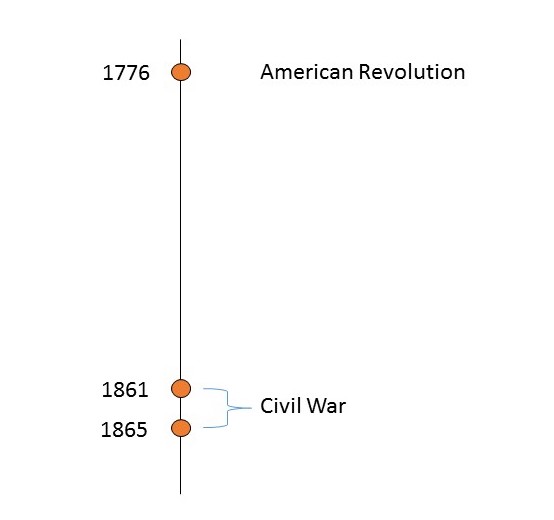
Clearly, Galois came of age in turbulent times. And rather than become just another genius who focused on his work to escape from the chaos around him—also known as “pulling an Einstein”—Galois actively engaged in politics. Influenced, no doubt, by his own father who’d been a supporter of Napoleon and leader of his town’s liberal party.

According to biographers Tony Rothman and John Derbyshire, Galois had a reasonably normal childhood, which quickly changed course while preparing to attend college. In short order, his father committed suicide, and he failed the entrance exams to the prestigious Ecole Polytechnique in Paris. He was accepted to a lesser university, the Ecole Preparatoire, but in time was expelled from school due to his politically charged criticisms of the school’s headmaster.

At this point, Galois did what any mathematical prodigy in his position would do: He joined the Artillery of the National Guard. Galois was arrested twice in the next year. The first time for threatening the life of King Louis-Philippe at a gathering of fellow republicans (who were generally against the monarchy). Acquitted on this account, Galois was arrested again several months later for wearing his National Guard uniform on Bastille Day. This sounds like a strange reason to be arrested unless you understand that the National Guard had been disbanded by Louis-Philippe six months earlier on concerns that they’d try to overthrow the monarchy. Also, the arrest may have had something to do with the fact that he’d gone full-blown Rambo, and at the time of his arrest, carried “a loaded rifle, multiple pistols, and a dagger.”

Following this second arrest, Galois languished in prison for the next nine months.

III. Galois’ Obsession

Trigger warning: the following section contains scary equations. Be advised, you don’t need to actually understand them for our purposes.

While in prison, Galois received a rejection letter from the Academy of Sciences where he’d submitted a mathematical paper the year prior. To understand the problem Galois tried to address in this paper, we must first recall some basics of algebra.

Most people have a general idea of what I mean when I say an “algebraic equation.” Like this:

x + 4 = 0

If I asked you to find the value of x that “solves” this equation, some could deduce that x = -4. That is, if you plug in -4 for x in the equation, it does in fact equal 0. If I had the following equation:

x + a = 0

The solution is just x = -a, where a is now a stand in for any number you’d like (4, 10, etc.).

If you ever took an algebra class in high school or college, you may have a hazy memory of more complicated equations, like the following:

This is the most general form of a quadratic equation. Here a, b, c could be any (fixed) numbers and x is the unknown variable.

Bonus points if you happen to recall that the equation above has the following ugly-ass solution for the unknown x:

Speaking of ugly, some folks may recall that there is a cubic equation that looks like this:

You probably never saw a full solution to it in one of your algebra classes it because it looks like this:

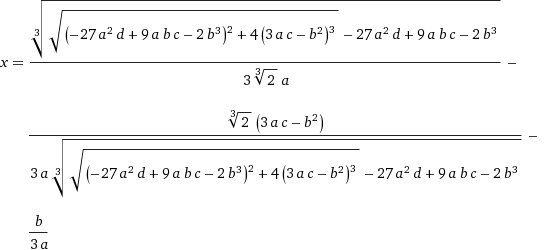
You clearly do not want to find yourself alone in a dark alley with that abomination of nature.

There is also the quartic equation (with four powers of x) and I’m not even going to try to write the solution for that equation here.

What’s the point of all this algebraic showmanship? Just this: for some kinds of algebraic equations, the universe has seen fit to provide us with handy formulas that can be used to solve for x. These work regardless of what the specific values of a, b, c, etc. are in those general equations above. Specifically, we have such formulas for quadratic, cubic ,and quartic equations.

Now interestingly, and clearly I’m using a very, very loose definition of “interesting” here, there is no general formula when the equation involves five or more powers of x (so called “quintic equations”). At least not one that would look like the formulas we saw above in terms of the sorts of basic operations you find on a calculator (±,×,÷, √, etc.).

This is the heart of the mathematical puzzle that Galois thought about in between his various acts of high treason:

Why are there “nice” formulas for the solutions of some kinds of equations (quadratic, cubic, and quartic) but not others (quintic, sextic, etc.)?

I know, I know. It literally sounds like the most boring puzzle anyone has ever posed in the history of the world. But to each his or her own, right? One person’s Sudoku is another person’s boring ass number crossword.

And to be clear, it’s boring because you don’t have any context for this problem. Many people who watch football couldn’t care less about the deeper nuances of the game. When a commentator like Jon Gruden starts talking about “the three technique” or “the five technique” some defensive lineman uses, most viewers’ eyes glaze over as they wait impatiently for Odell Beckham made a one-handed catch. But play or coach football for years and these sort of more technical features of the game become fascinating.

If you’ve only ever solved a handful of algebraic equations in your life, you are like the casual football fan. But if you are a full bore math nerd like Galois, solving algebraic equations for the umpteenth time eventually gets boring. So what do you do? You look for deeper, more fundamental problems. You start to see math the way Gruden sees football.

Galois became obsessed with this puzzle. And despite his troubling personal life he made more progress on the problem than any of the more prominent and senior mathematicians of his day. Ultimately, Galois succeeded in building the foundations of what would be later called “Galois Theory.” Now the details of Galois Theory are too dense and abstract for our purposes here. But at least you can start to understand the “kind” of problems that mathematicians work on. Galois wasn’t interested in solving a particular equation. He was after something more fundamental, something that went to the heart of why you could even solve certain equations in the first place.

But Galois never actually finalized his theory. He left the ideas that his contemporaries pieced together. Why? Because a month after being released from prison, Galois took part in a duel. And I don’t mean like a Math Off.

IV. Going Out with a Bang

It’s hard for us modern folks to wrap our heads around the idea of dueling. Shooting someone seems like an unnecessarily severe way to resolve a simple dispute. Though—to be fair—the Rock, Paper, Scissors option only became available to the West much later. It may not be a coincidence that the last fatal duel in England took place in 1845, just three years after the founding of the Paper Scissors Stone Club in London (in 1842).

As the handful of folks who actually got Hamilton tickets know (looking at you, Mike Pence), Americans loved a good duel. But nobody dueled quite like the French. According to one estimate:

In France during the reign of Henry IV, more than 4,000 French “gentlemen” lost their lives in an eighteen-year period.

King Henry had a dueling epidemic on his hands. And though King Louis XIII outlawed dueling in 1626, the next Louis (XIV) still had to contend with an estimated 10,000 duels.

No one is actually sure who Galois dueled. One possible adversary was a man named Pescheux d’Herbinville, no doubt the Frenchiest sounding name I’ve ever seen. Look at that extra “d” just appended to the front of the perfectly adequate surname “Herbinville.”

It’s not even clear why Galois participated in a duel, though there is reasonable speculation that it was related to a love affair with woman named Stephanie Dumotel. In a letter to friends Galois wrote:

I beg patriots, my friends, not to reproach me for dying otherwise than for my country. I die the victim of an infamous coquette and her two dupes. It is in a miserable piece of slander that I end my life. Oh! Why die for something so little, so contemptible?

There are two things to learn from Galois’ words here: 1) Galois was clearly a bit of a drama queen; 2) coquette is by far the greatest term to be used in describing a flirtatious woman that you will ever find.

But it was more than just the coquette. As Derbyshire writes, “It is likely that Galois had, in some sense, given up on life. The death of his father, the rejection of his paper (following on the misfortunes of its previous submission), his unrequited love for Stephanie, his own small-to-nonexistent employment prospects, the months of confinement, the wretchedness of Paris during the [Cholera] epidemic—it was all too much for him.”

Maybe Galois just woke up one morning, decided he’d had enough, and went off to challenge the first white gloved dope he met on the street to a life or death duel. If only they’d had Facebook Live back then, we’d probably have much more of the story.

But instead, all we have is this entry in a French paper from June 4, 1832, describing the end result:

A deplorable duel yesterday has deprived the exact sciences of a young man who gave the highest expectations, but whose celebrated precocity was lately overshadowed by his political activities.

V. Mainstreaming Galois

In his “famous” book Men of Mathematics, E.T. Bell wrote:

Abel was done to death by poverty, Galois by stupidity. In all the history of science there is no completer example of the triumph of crass stupidity over untamable genius than is afforded by the all to brief life of Evariste Galois. The record of his misfortunes might well stand as a sinister monument to all self-assured pedagogues, unscrupulous politicians, and conceited academicians. Galois was no “ineffectual angel,” but even his magnificent powers were shattered before the massed stupidity aligned against him, and he beat his life out fighting one unconquerable fool after another.

In other words, Bell assures Galois:

Bell doesn’t want Galois’ legend, that of the genius who died too young because of stupidity, to be tainted by anything suggesting that Galois was a willing participant in the less flattering events in his life.

But I, like Rothman, think Bell has it all wrong. Galois’ story is fascinating precisely because of his human imperfections: both his major flaws and his minor peccadillos.

In fact, I think the Galois story should go mainstream. Seriously, the mathematician John Nash develops schizophrenia and he gets a hollywood blockbuster. The mathematician Alan Turing decodes some Nazi messages, while repressing his homosexuality, and he also gets a Hollywood blockbuster.

When will Hollywood make a movie about Evariste Galois? The radical mathematical man who defied kings, spurned coquettes, and died defending his honor.

Seriously, Matt, Ben, come greenlight this thing. Netflix, we can talk too. ⧫

---

The details of Galois’ life are most carefully described by Tony Rothman in Genius and Biographers: The Fictionalization of Evariste Galois whom I’ve relied on heavily along with John Derbyshire’s Unknown Quantity: A Real and Imaginary History of Algebra. The latter especially being the sort of fun mix of mathematics and historical vignettes that I assume no reader of this piece is, has, or ever will consume.