The {Hairy} Ball Theorem: Abstract Math that Won’t Drive You Nuts

Math often gets a bad rap. In school, it’s a class to be suffered through, full of dull things you just have to remember and the often-asked question: When are we going to use this in real life?

Math is s a big part of the SAT, ACT, GRE, and other standardized tests that no one enjoys taking. In many corporations, you have entire departments that do nothing but math so that everyone else doesn’t have to. Finally, everyone seems to agree that there are “math people” and everyone else who must be “bad at math.” How comfortable can you feel about something that you’re pretty sure lots of people are just genetically bad at?

I happen to like math.

Sure, I’m probably biased because I am one of those “math people” who is “good at math.” But I like math not because I enjoy memorizing multiplication tables or equations—at its core, math isn’t about memorization. It’s about relationships, and logic, and applying patterns of thought to different concepts.¹

Mathematicians often talk about the beauty and elegance of a theorem or proof in the same way others might talk about an art show, a concerto, or a ballet performance. (Or even compare the thrill of intellectual discovery to the exhilaration of a clutch, game-winning play!)

This is what most people think of if you tell them to combine ‘art’ and ‘math.’ Mathematicians consider something else entirely: To them, math *is* art.

Albert Einstein once wrote, “Pure mathematics is, in its way, the poetry of logical ideas.”

He was paying tribute to the work of a German mathematician, Emmy Noether, after her death. In the obituary that he wrote, he noted that her ability to articulate concepts of advanced algebra helped to advance the field of mathematics through elegantly formed arguments and shaped the understanding of future generations of mathematicians.

Now, it’s not bragging to say that I share (some of) Einstein’s love for the art of logic that is mathematics.

But I am no Albert Einstein.

Which is why I am instead writing to you, here, about the Hairy Ball Theorem.

Yes, it’s a real theorem, and yes it’s really called that. Feel free to Google it: you (probably) won’t get NSFW results. [Editor’s note: The Prompt assumes no liability for any search results that may turn up because of your own browsing history.] What makes it interesting is not just its name. It happens to be a great way to show how abstract thinking like math can reveal new and interesting things about the world you live in.

Let’s cut to the chase and dive into the mysteries of the Hairy Ball.

First off, this is a theorem, and every theorem needs a definition. But this is an article on The Internet, so we can toss the “textbook definition” into a footnote for people who want it.² Here’s the everyday expression:

You can’t comb a hairy ball flat.

Underwhelming, perhaps. Maybe some pictures will help.

Start with a ball. Then add hair: the spiky kind so that your ball looks more like a sea urchin.

The name’s Ball. Hairy Ball.

What happens if we try and comb this hairy ball flat with smooth strokes of our comb? Let’s keep things simple and just comb flat one way, from left to right, spinning the ball as we go.

This sort of thing is what happens when you refuse to listen to people who tell you that you can’t do something.

We’re doing OK. Take that, theorem! We’ve got the middle, let’s start getting to the top and bottom. As we go, we notice the closer we get to either pole, the more curved the ball gets. We’re still combing flat, but our combed hair is starting to swirl in a curve instead of staying left-to-right straight.

Next time I need to draw a lot of arrows, I’m hiring a professional illustrator.

As we hit the very top or bottom of the ball, we’ve got a problem. The further up or down we go, the more and more we’re starting to curl into a whirl until suddenly …

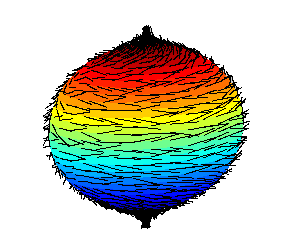
In a fit of laziness, the author ends up heading to Wikipedia.

The hair at the top and bottom points will stick straight out, nothing flat about it. And it wouldn’t matter if we tried a different approach than starting left to right. No matter how we try, we wouldn’t be able to get everything to lie flat. There’s always going to be at least one point that sticks up.

Interestingly enough, you know what shape doesn’t have this problem?

A donut.

Math person or not, I think we can agree that a hairy donut is best left as a mathematical curiosity. (I bet Portland sells them though.)

What’s going on? There is something inherently different about the surface of a ball and a donut that cause them to have these funny behaviors. Topology is the branch of mathematics that studies surfaces like these and their properties. It turns out that the hole in the donut gives it a special property that a solid ball doesn’t have. You can comb a hairy donut flat, but a hairy ball? Forget about it.

All of this is more interesting if we stop thinking about actually hairy balls and think instead about situations that behave like hairy balls—in the mathematical sense, that is.

The theorem says that any of these mathematical situations will always have at least one spot that equals out to zero, which is the numerical equivalent of the “tufts” at the North and South Poles of our hairy ball. (There could be many such spots! There were two in our exercise above, but the theorem indicates there always has to be at least one.)

“Wait, there’s a hairy tuft where?!”

So what types of zero values make for real-world, non-hairy applications?

• If you think of the hair as wind swirling across Earth, the swirls around a zero point of wind represent a cyclone. So the Hairy Ball Theorem means there always has to be a cyclone somewhere on Earth at all times.³ (Check out this amazing tool to see the wind patterns of the Earth in near-real time, and look at those swirls!)
• Nanotechnology relies on building things with tiny objects you cannot see. Scientists took advantage of the Hairy Ball Theorem to understand that molecules arranged on the surface of gold-plated spheres would have to “stick up” at each pole, creating spots where the molecules could easily link up or react. The building blocks of the microscopic world are within our reach!
• Antennas are metal devices that radiate (or receive) electromagnetic signals. Creating an antenna that radiates a coherent signal at equal power in all directions is impossible. Think of the signal as a sphere spreading out around the antenna; at some point in time the signal will have to be zero, ruining the ideal coherent antenna. This seems like a bummer, but often times it’s great to know that you can stop chasing down the perfect setup and simply be happy with what you’ve got.

These are technical applications to be sure, but they’re all examples of how the abstract world of math can tell us details about the very concrete world in which we live.

You don’t even need to go as far as topology to make this connection: If you want to budget and pay off your student loans faster, you’d better know some algebra. If you’re trying to hustle your way through a pool game (or trying to figure out if you can get a couch up your stairs), you’ll benefit from some geometry. And if you want to have any chance of making sense of the increasingly data-filled reporting in the media, a little bit of statistics will be your friend.

But being able to think logically, adjust your line of thinking to new information, and use patterns to predict how something will turn out?

These are the true real-world gifts of embracing the world of math.

So please, my friends, I implore you: the next time you think to yourself, “I’m not a math person,” think back to the time you were able to get a grip on the Hairy Ball Theorem. You might just see things in a whole new light.

Footnotes:

1 I often see a lot of griping on social media from parents complaining about their kids’ “new math” homework, where it takes 20 steps to multiply two two-digit numbers and asks their kids to “explain how they know.” “Why,” cry the hapless parents, “can’t they just do the math and write down the answer?”

Well, the new math is trying to instill number sense into children at a young age, teaching them to think about numbers in an abstract fashion instead of just memorizing a process. Kids who learn the “new” way of multiplying two-digit numbers now have fewer issues later with advanced, but similar, topics such as multiplying polynomials in algebra. They already understand multiplication as a concept that applies to lots of scenarios, rather than a process that has to be learned over and over each time.

And in a world that’s become more technical by the month, we really, really need to get the next generation prepared for abstract thinking early if we want them to be able to build the algorithmic, social-media-fueled nursing homes that we will surely be shuttled off to at some point. (Also to maintain our dominance of global tech developments, etc. etc.)

2 If you’re down here, you asked for it: “There is no nonvanishing continuous tangent vector field on even-dimensional n-spheres.” Yeah, I prefer the Hairy Ball Theorem too.

3 The cyclone doesn’t have to be a catastrophic storm. Cyclone is just the word for a spot of low pressure surrounded by circling air of higher pressure.